2026 Forfatter: Leah Sherlock | [email protected]. Sist endret: 2025-06-01 06:58:43
Dagens musikalske praksis er basert på et system som er en rekke lyder. Det er visse høyhusforhold mellom dem. Deres plassering i høyden kalles vanligvis skalaen. Hver lyd i den er et trinn. Det er omtrent hundre lyder i hele skalaen til dette systemet. Frekvensene deres varierer sterkt og er konsentrert i området 15-6000 svingninger per sekund. Disse lydene er hørbare for det menneskelige øret. Og den nøyaktige definisjonen av høyden deres avhenger av graden av utvikling av det musikalske øret.
De viktigste trinnene på skalaen er navnene på hovedtonene, fra «Do» til «Si». Og hva er så den naturlige skalaen? Og hva er forholdet mellom lyder i den? Og hvilken rolle spiller deltoner i den?
Definition
En naturlig skala er et lydområde som inkluderer grunntonen og harmoniske overtoner (deres andre navn er overtoner).
Vibrasjonsfrekvensene til lyder her samhandler på en slik måte at det oppnås en naturlig tallserie: 1, 2, 3, 4 … På grunn av tilstedeværelsen av overtoner kalles denne skalaen den naturlige overtoneskalaen.
Noen overtoner overskrider tonehøyden til hovedlydene, mens andre overtoner,tvert imot, de er underlegne i denne henseende.
Hva er partialer?
Den naturlige skalaen er også preget av tilstedeværelsen av deltoner. Tallet deres i forskjellige oktaver og fra hver tone er forskjellig:
| note | octave | counter-oktav | stor oktav |
|
C |
32 | 65 | |
| C | 34 | 69 | |
| D | 36 | 73 | |
| D | 38 | 77 | |
| E | 20 | 40 | 82 |
| F | 21 | 42 | 87 |
| note | octave | counter-oktav | stor oktav |
| C | 32 | 65 | |
| C | 34 | 69 | |
| D | 36 | 73 | |
| D | 38 | 77 | |
| E | 20 | 40 | 82 |
| F | 21 | 42 | 87 |
| F | 23 | 44 | 92 |
| G | 24 | 46 | 103 |
| G | 25 | 49 | 110 |
| A | 27 | 51 | 116 |
| A | 29 | 55 | 118 |
| B | 30 | 58 | 123 |
Denotasjoner: A - la; D - re; E - mi, F - fa, G - s alt, B - si;- skarp.
En lydbølge har en veldig kompleks konfigurasjon. Årsaken til dette er (i eksemplet med en gitarstreng): det vibrerende elementet (strengen) vibrerer, brytning av lyd skapes i like proporsjoner. De produserer uavhengige vibrasjoner i kroppens totale vibrasjon. En annen bølge skapes, identisk med lengden deres. Og de genererer delvise toner.
De angitte tonene kan variere i høyde. Tross alt har dynamikken til oscillasjonene til bølgene som dannet dem forskjellige parametere.
Hvis strengen bare dannet grunntonen, ville bølgen ha en enkel oval form.
Den andre deltonen kommer fra halvparten av den første lydbølgen til strengen. Bølgelengden er dobbelt så lang som bølgenhovedtone. Og når det gjelder vibrasjonsfrekvens, er den dobbelt så stor som hovedtonen.
Bølgestrømmer fra den tredje lyden er allerede tre ganger mer dynamiske enn bølgene til den første lyden. Fra den fjerde - fire ganger, fra den femte - fem, osv.
Startlyden (grunntonen), nærmere bestemt antallet vibrasjoner, kan vises som en enhet. Det antallet svingninger av de resulterende tonene kan uttrykkes i enkle tall. Deretter oppnås en enkel aritmetisk serie: 1, 2, 3, 4, 5…. Dette er allerede en naturlig lyd. Det gjenstår å håndtere konstruksjonen.
Bygg spørsmål
Hvordan bygge en naturlig skala? For å svare på dette spørsmålet tilbys det enkleste eksempelet.
Hovedtonen her er tonen "Do", plassert i en stor oktav. Fra den organiseres konstruksjonen av en lydserie som har frekvenser i henhold til det angitte mønsteret
Følgende resultat av denne konstruksjonen er oppnådd:

En slik kompleks struktur av den naturlige skalaen fra en streng blir ikke oppfattet av en person bevisst. Og følgende årsaker vises her:
1. Mange lyder har en lignende struktur.
2. Amplitudene til overtoner er betydelig dårligere enn amplituden til hovedfrekvensen som kommer fra strengen.
Bygger fra notater

Du kan bygge et naturlig lydområde fra hvilken som helst tone. Det er også viktig å vurdere tone. Det kan være mindre eller større. For det første er byggeordningen som følger:
T - P - T - T -P- T - T
Opplegg forden andre er som følger:
T - T - P - T - T - T - P
Notasjon her: T - tone, P - halvtone.
Dermed, når man bygger fra "A" i moll, får man følgende bilde:
A - B - C - D - E - F - G - A
Samme rad, men i et stort scenario, ser slik ut:
A - B - C - D - E - F - G - A
Seddelen som serien er bygget opp fra kalles tonic.
Følgende er eksempler på konstruksjon fra "Re" og "Fa".
Arbeid fra "Re"
Den naturlige skalaen fra "Re" er også bygget avhengig av toneart. Mindre bygning gir følgende resultat:
D - E - F - G - A - A - C - D
I musikkboka står det slik:

I hovedscenarioet er situasjonen som følger:
D - E - F - G - A - B - C - D
Og i musikkboken (eller "Guitar Pro"-programmet) legges oppføringen inn som følger:

Men det er flere nyanser. Den samme skalaen kan eksistere i harmonisk modifikasjon. I den vises en ekstra halvtone før tonika.
I det mindre eksempelet ser bildet slik ut: D - E - F - G - A - A - C - C. Lyden er orientalsk.
Arbeid fra Fa
Naturskalaen fra "F", bygget etter durskjemaet, har samme fortegn som mollskalaen fra "D". Dette er to parallellnøkler.
Og hovedstrukturen til den naturlige skalaen, bygget fra "F", er som følger:
F - G - A - A - C - D - E - F
Innspillinger på musikalske linjer oppnås som følger:

Mindre konstruksjonsmønster:
F - G - G - A - C - C - D - F
Følgende betegnelser er oppnådd på de musikalske linjalene:

Her er skiltene de samme, men er angitt med flater: A - flat=G. B flat=A. D flat=C. E flat=D.
På naturlige intervaller

Det er bare tilsvarende intervaller på hovedtrinnene til naturlige strukturer. Disse inkluderer både den utvidede fjerdedelen og den reduserte femten.
Tot alt antall intervaller med samme trinnparameter er alltid identisk med antall hovedtrinn. Og ethvert slikt intervall bygges på et annet trinn.
I parallelle tangenter er gruppen av intervaller alltid den samme. Men trinnene de er hevet på varierer.
Følgende tabell er gitt for å vise disse prinsippene:
| Intervals | Hovedtypene deres | Trinn med deres tilstedeværelse | nummeret deres |
| Naturlig. major | Naturlig. mindre | ||
| Prima | Ch. | I det hele tatt | I det hele tatt |
| Second | M | 3 og 4 | 2 og 5 |
| - »- | B | 1, 2, 4, 5 og 6 | 1, 3, 4, 6 og 7 |
| Thirtia | M | 2, 3, 6 og 7 | 1, 2, 4 og 5 |
| - »- | B | 1, 4 og 5 | 3, 4 og 7 |
| Quart | Ch. | 1- 3, 5 -7 | 1 - 5, 7 |
| ….. | Uv. | 4 | 6 |
| Quint | D. | 7 | 2 |
| ….. | Ch. | 1 - 6 | 1, 3-7 |
| Sexta | M. | 3, 6, 7 | 1, 2 og 5 |
| -» - | B. | 1, 2, 4 og 5 | 3, 4, 6 og 7 |
| Septima | M. | 2, 3, 5-7 | 1, 2, 4, 5 og 7 I |
| - »- | B. | 1 og 4 | 3 og 4 |
| Octave | Ch. | I det hele tatt | I det hele tatt |
Notasjon i tabellen:
B er stort. M er liten. H -ren. Uv - økt. Mind - redusert.
About tone change signs
Disse tegnene er skarpe tegn (angitt med symbolet, som betyr en økning med en halv tone) og flat b (angitt med symbolet b, de indikerer en reduksjon med en halv tone). I det naturlige intervallet settes de ikke samtidig.
Det er en viktig nyanse her: tonen "La" har ikke en spiss, som er den kvint i rekkefølgen.
Denne nyansen indikerer at i tonearten, der det er minst 5 skarpe punkter, vises ikke dette intervallet.
Så den store sjette (b.6) fra "La" (A - F) finnes bare i dur og moll, der det er maksim alt 4 skarpskår.
Følgende toner faller inn under dette kriteriet:
- Major: G, D, A og E.
- Minor: Em, Bm, Fm, Cm
Jobber med intervaller uten stigende eller fallende tegn, må du beregne hvilken lyd som først dannes her med dette tegnet. Videre arbeid bygges etter angitt prinsipp.
Eksempel: søk etter en toneart med en liten terts E - G. Du kan følge kvintsirkelen mot skarpene. Da skal skiltet vises ved lappen "Sol". Men han dukker ikke opp i denne posisjonen. Da inneholder ikke strukturer med minst 3denne tredje.
Du kan gå i samme sirkel, men til leiligheter. Da skal leiligheten dannes nær "Mi". Det er han imidlertid ikke. Da vises ikke den angitte avstanden i konstruksjoner der minimum er 2 leiligheter.
Som et resultat av søket, er den mindre tredje E - G i slike mindre og større strukturer, der:
- ingen tegn for nøkkel;
- det er 1-2skarp;
- det er 1 leilighet.
Deretter er tastene spesifisert med navn og trinnene som dette intervallet er hevet på.
Følgende prinsipp vil hjelpe med dette: det er 7 hovedtrinn i harmoni. Og her er det 7 sekunder, samme antall tredjedeler og andre intervaller. De kan variere i toneverdi. Denne faktoren bestemmes av konstruksjonen fra et visst nivå.
Eksempel: det er større og mindre strukturer. Her dukker det mindre sekundet opp to ganger. I det første tilfellet, ved 3 og 4 trinn. I det andre - på 2. og 4. trinn.
Så er det bare store sekunder i kø på de fem andre trinnene.
Musikkøving
Det finnes instrumenter som skiller seg ved at kun den naturlige skalaen trekkes ut på dem. Det handler om:
- Horn og fanfare.
- Alle typer horn.
- Rør.
- Horn.
- En overtone-fløyte, for eksempel russisk Kalyuka.
Det vil si at de hovedsakelig er representanter for kategorien blåseinstrumental. Og den naturlige skalaen til blåseinstrumenter fra denne listen blir ofte oppfattet som et rent system. Dette er en feil.
Så ved ren stemming dannes m.7 (moll kvint) ved å legge til kap.5 og kap. 3 (rene legger sammen: en femtedel og en liten tredjedel). Frekvensparameteren til lyden er 1017, 6 c. Og i naturlig syvende når den 968,8 c.
Den angitte skalaen brukes ofte i etnisk sang. Eksempler:
- indisk raga.
- Tuvan halssang.
- Sang av den afrikanske stammen Kosa (vekt på første stavelse).

Akademisk musikk kjenner sjeldne eksempler på bruk av den naturlige skalaen. Den mest slående av dem er den første og siste delen av Brittens Serenade. Der spilles en hornsolo.
Anbefalt:
Hvordan tegne hår naturlig og vakkert
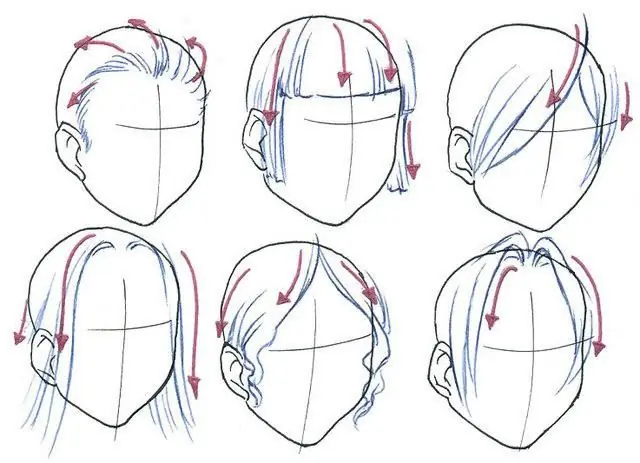
Å tegne en person er veldig vanskelig, spesielt hvis det er et portrett, men ingenting kan sammenlignes med kompleksiteten til bildet med hår. Virker som en ganske enkel detalj helt til du begynner å male den. For å gi håret et naturlig utseende, må du prøve. Det er ikke noe vanskelig å tegne en uforståelig floke på hodet, som ikke vil se for naturlig ut. Men å lage grasiøse flytende tråder er ikke en lett oppgave
Hva er nøtter i poker: konseptet, den best mulige kombinasjonen, eksempler

Mange nykommere til poker eller fans som spiller dette spillet i selskap med venner, for hvem teorien om poker er en "mørk skog", har ingen anelse om mange av begrepene som brukes i spillet. Et av konseptene vil bli diskutert i vår artikkel. Vi vil fortelle deg hva nøtter er i poker, vurdere klassifiseringen, hvordan du identifiserer dem og spiller dem riktig. Vi vil også gi eksempler på noen nøttekombinasjoner og analysere hvordan man kan vinne mange sjetonger hvis nøttene faller
Vurder actionfilmer: fra naturlig massakre til en ny klassiker i sjangeren

Tradisjonelt er alt kjent i sammenligning, så i filmindustrien får denne vanlige setningen en spesiell betydning, som bestemmer vurderingen til en film. Rating actionfilmer er et mål på popularitet, evaluering, prioritering og til og med klassifisering. Det etableres ved å spørre en imponerende målgruppe av seere eller en mer beskjeden - eksperter
Hvordan tegne en frosk: naturlig og tegneserie
Ved å følge enkle trinnvise instruksjoner vil vi forstå hvordan man tegner en frosk i forskjellige stiler. I den første mesterklassen vil hun se ut som en ekte, og i den andre vil hun bli en morsom tegneseriefigur
Umber: naturlig farge og nyanser

Umber er en farge folk får fra naturen selv. Varm jord, trestammer, duftende krydder, lysninger av sumper, varme dyrepelsverk - denne varme fargen fremkaller slike assosiasjoner, og det er for deres bilde at den ofte brukes

